|
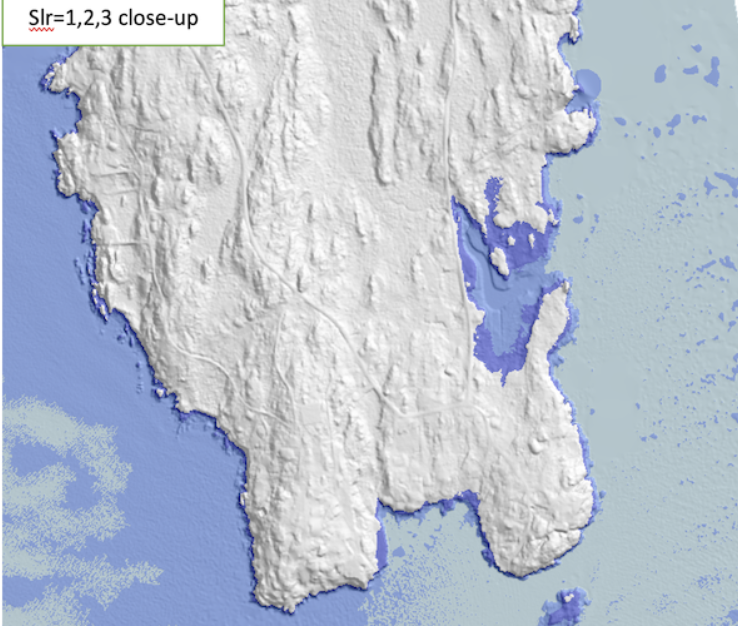
We describe an efficient algorithm for
computing flood maps caused by overlapping sea-level rise (SLR) and
storm surges, based on the method used by the second New York City
Panel on Climate Change (NPCC2). Presently, areas at risk of storm
flooding are given by FEMA's base-flood elevation (BFE) maps which
depict the flooded areas as well as surge heights. Given a grid
digital elevation model (DEM), a BFE map and an arbitrary
amount x of SLR, our algorithm computes what part of the
terrain gets flooded if a sea-level rise of x overlaps the
storm surges in the BFE map.
As an example, we present results for Lincoln County in Maine, using a
2m resolution raster DEM obtained from LiDAR data, totaling 919
million points. Our algorithm overlaps FEMA's 1%-annual-chance storm
BFE map with an arbitrary SLR in less than 100 seconds on a laptop,
and produces results that are very close to the ones obtained using
NOAA's protocol in ArcGIS, which runs for hours.
|
 |
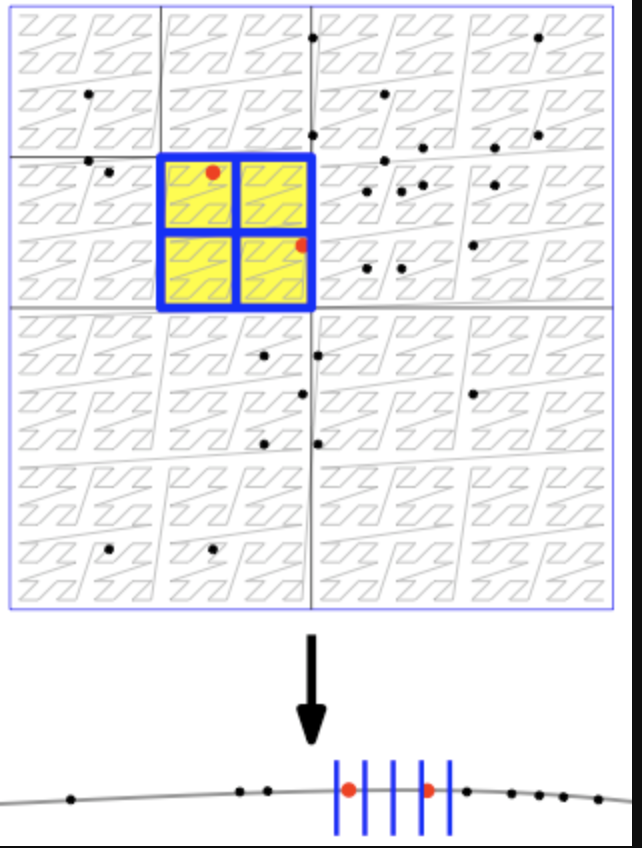
The viewshed of a point v on a
grid terrain T,
viewshedT(v), is the set of grid points
in T that are visible from v. We describe a novel
algorithm for computing viewshedT(v) using a
double-resolution approach: Given a parameter k that
represents the block size, we create a grid T' which is a
smaller, lower-resolution version of T, such that each
point in T' corresponds to a block of
|
|
|
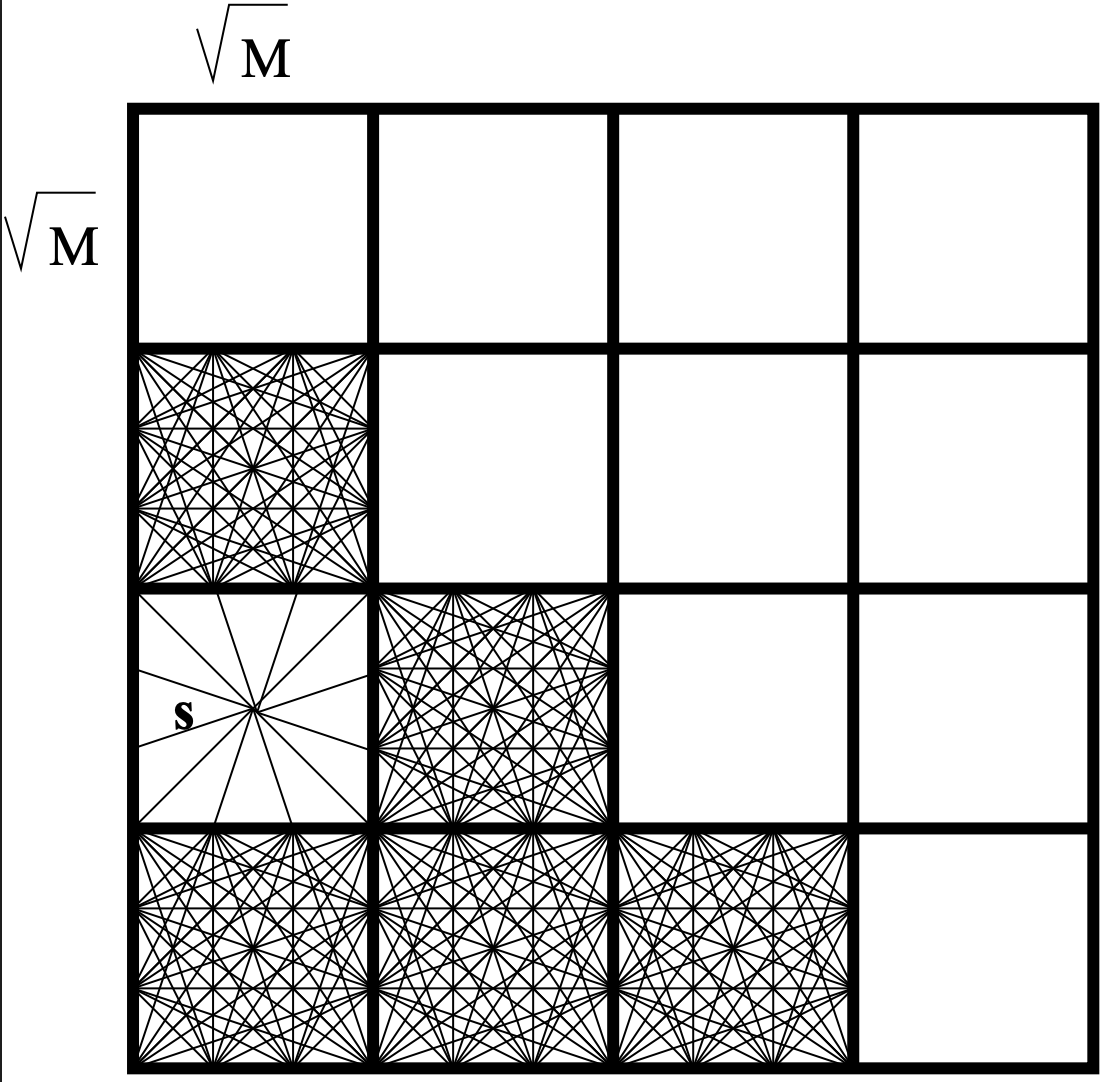
We consider the problem of building a quadtree subdivision
for a set of edges in the plane. That new cache-efficient
algorithm that we propose has two steps: First, build a
quadtree on the vertices corresponding to the endpoints of
the edges. Second, compute the intersections between the
edges and the cells in the subdivision. We propose a new
data structure, the K-quadtree: for any
k>=1, a k-quadtree is a linear compressed
quadtree that has O(n/k) cells
with O(k) points each. We show how to build a
k-quadtree cache-efficienctly. As an application, we
consider one of the basic problems in spatial data
structures, map overlay, and implement it via
k-quadtrees. We report experimental results.
|
|
|
We describe an algorithm to compute the viewshed with
linear interpolation and without using any
approximation. The algorithm is based on computing and
merging horizons, and in practice it is faster than our
previous viewshed algorithms, while being more
accurate. We prove that the complexity of horizons on a
grid of n points is O(n), improving on the
general O(n \alpha (n)) bound on triangulated
terrains.
|
|
|
We describe the design and engineering
of three new algorithms for computing viewsheds on massive
grid terrains. The first two algorithms sweep the terrain
by rotating a ray around the viewpoint, while maintaining
the terrain profile along the ray. The third algorithm
sweeps the terrain centrifugally, growing a star-shaped
region around the viewpoint, while maintaining the
approximate visible horizon of the terrain within the
swept region. On a terrain of n grid points,
these algorithms run in O(sort(n)) I/O's in the
I/O-model if Agarwal and Vitter. This algorithm runs in
O(n) time and O(scan(n)) I/O's and is cache-oblivious.
|
|
|
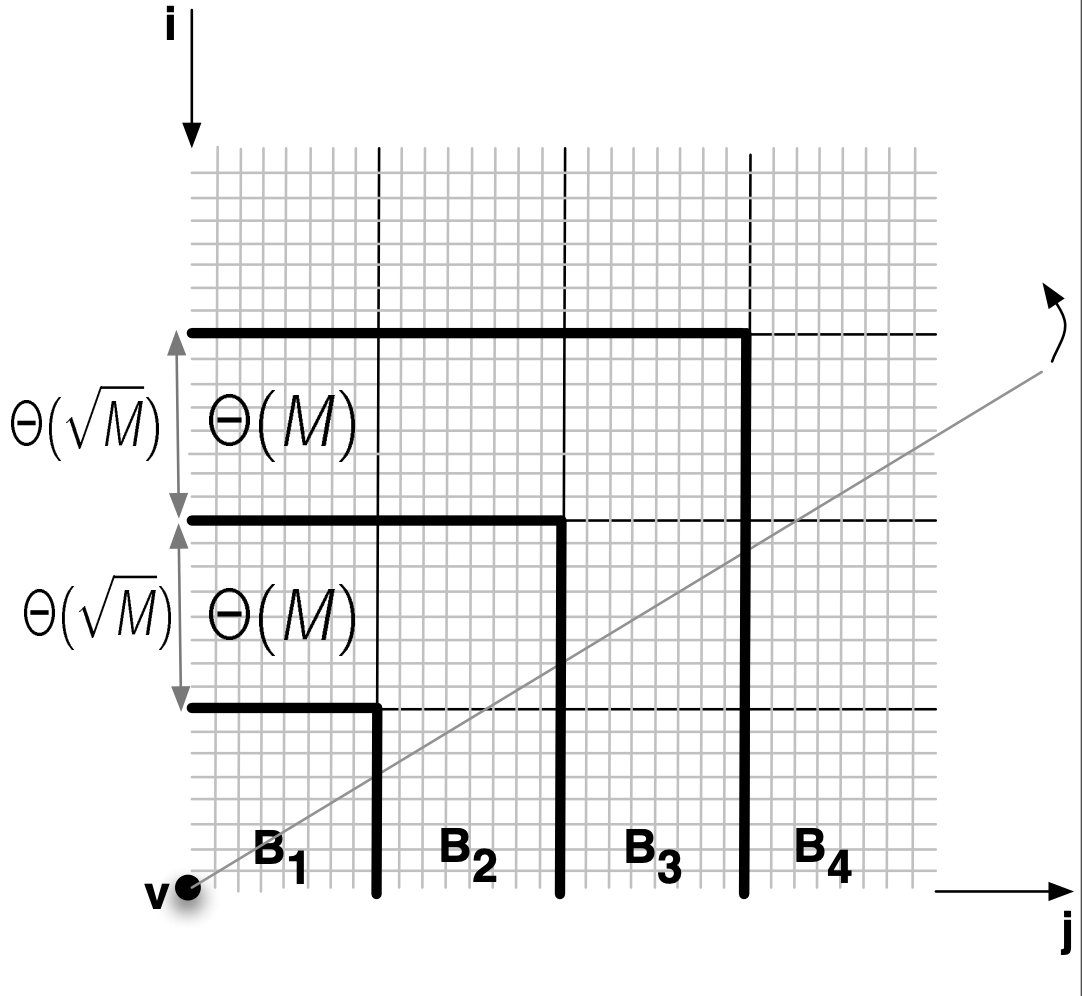
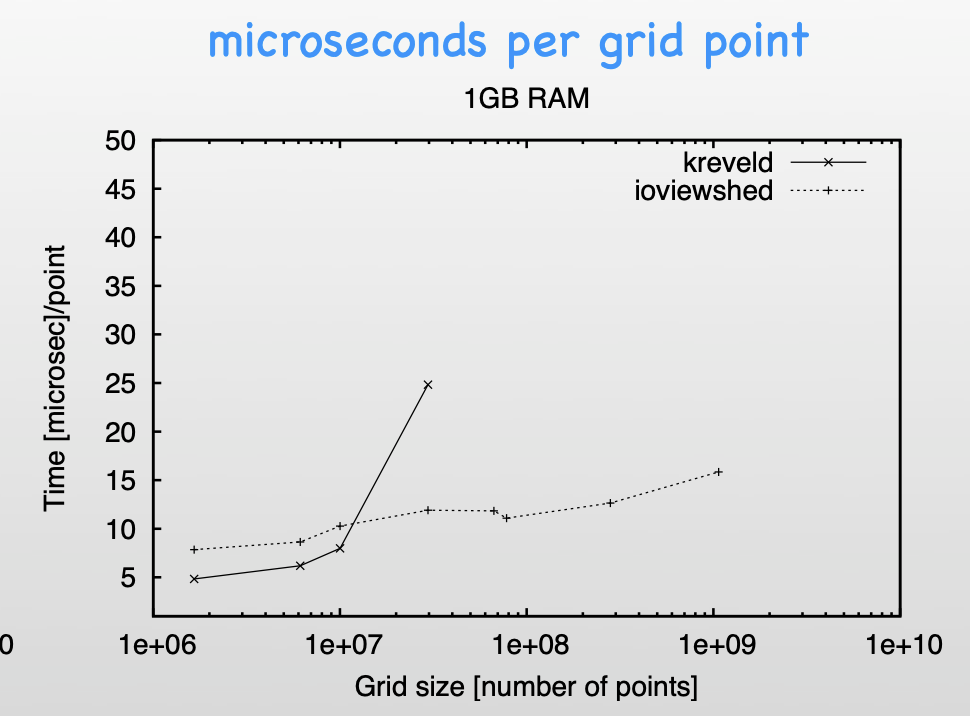
Given a terrain T and a point v, the viewshed of v is the
set of points in T that are visible from v. We consider the
problem of computing the viewshed of a point on a very large
grid terrain in external memory. We describe an algorithm for
this problem in the cache-aware and cache-oblivious models,
together with an implementation and an experimental
evaluation. We ported the algorithm to GRASS, where it was
adopted as one of their core
modules: r.viewshed
|
| Our module Terracost computes least-cost surfaces on massive grid terrains and is motivated by cost analysis in GIS. Computing a least-cost surface corresponds to the problem of computing multi-source shortest paths (MSSP) using an implicit graph given by grid topology. From a memory point of view, MSSP has a larger cache footprint and poorer spatial locality compared to SSSP. When the standard MSSP algorithm runs in external memory, it starts to thrash. Terracost's idea is to partition the graph in subgraphs with small boundaries, and replace each subgraph by a complete graph on its boundary vertices. The resulting graph has fewer vertices, preserves shortest paths, and the computation can be performed I/O-efficiently. Terracost is available as r.terracost in GRASS (extension library).
|
| The grid is the most widely used terrain model because of its simplicity, but can have significant space redundancy. TINs (triangular irregular networks) have the potential of being more space efficient than grids, especially for very large terrains. In this project we took a first step at simplifying a grid terrain into a TIN within a specified error threshold using an approach that scales to terrains that are arbitrarily larger than main memory. Our module, r.refine can work standalone or as an addon in GRASS open source GIS.
|