Patterns in mathematics: Do patterns have to continue? Could there be a list of numbers which seems to follow a pattern for 1,000,000 terms and then breaks down? How would you know? This unit may include a slight revision of the US currency system.

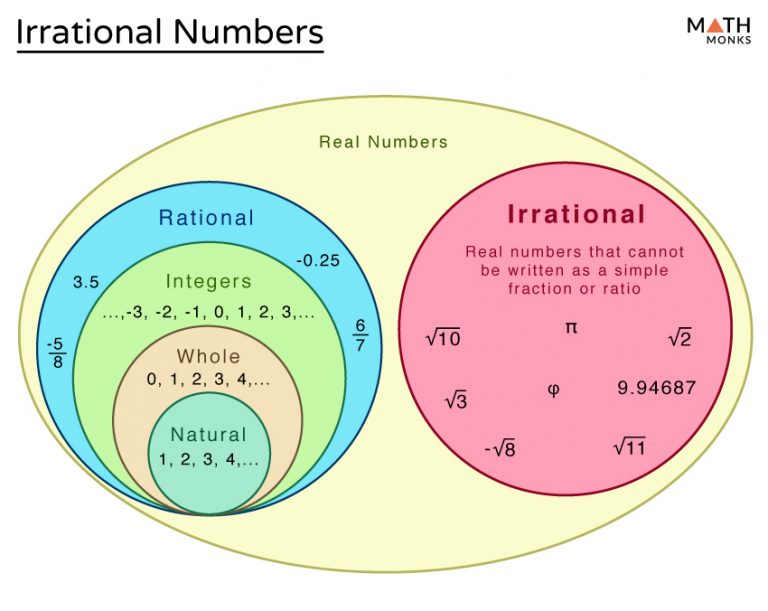
Operations and Number Systems: We use integers and properties of integers without thinking about them. What makes a number system? What properties of the integers are important? Could you have a number system where the product of two non-zero numbers equaled zero? Wouldn’t that be interesting! How do you show that a number is irrational? Why is the square root of 2 irrational? Why is e irrational? It’s actually a lot harder to show that pi is irrational!

Symmetry: How is symmetry mathematical? Can we use symmetries as a tool to distinguish between different objects? The mathematical term for something which can be used to differentiate between objects is an invariant. Given a set of symmetries, can you find an object which has exactly those symmetries? We will introduce the notion of a mathematical group which will give us the framework to discuss symmetries of different objects.

Cryptography: Why is your communication over the internet secure? How is cryptography based in mathematics? How does one attempt to break an encryption scheme? You might be surprised that the answer includes factoring, and factoring techniques unlike any you ever thought about! This unit is an application of our work on number systems and groups.

How do we compare the sizes of infinite sets?: Are there more integers or positive integers? More integers or rational numbers? More even integers or odd integers? More rational numbers or irrational numbers? What do these questions even mean for infinite sets? To answer these questions (and more) we will study functions in new non-calculus ways. We will see that certain types of functions form a number system of their own.