Ultracold Fermionic Atoms Team up as Molecules: Can They Form Cooper Pairs as Well?

The behavior of strongly interacting degenerate Fermi gases may hold clues to the universal behavior of many-body systems.

What a difference is made by one-half quantum unit of spin. Atoms with integer spins--bosons--can collapse into a common ground state when sufficiently cold; the result is a collective state known as a Bose-Einstein condensate (BEC). But atoms with half-integer spins--fermions--are excluded from occupying the same quantum states. The lowest-energy configuration they can reach is to fill all levels up to the Fermi energy--the highest level that would be occupied at absolute zero.

It was formidable enough to form a BEC. Creating a degenerate Fermi gas proved even more difficult, largely because Fermi statistics prevents identical particles from participating in the kind of head-on collisions required for the evaporative cooling that takes a gas to ultracold temperatures. The cooling problem was solved, and a degenerate Fermi gas formed, in 1999 by a team from JILA, NIST and the University of Colorado, all in Boulder (see Physics Today, October 1999, page 17).

Since then, a number of groups around the world have built up the expertise to form degenerate Fermi gases as well as BECs. The door is open to explore further the interface between the bosonic and fermionic worlds. Recently several groups have created bosonic molecules from fermionic atoms, and they have found that the molecules live long enough to allow the formation of a molecular BEC. It should now be very interesting to study what happens when ultracold bosonic molecules dissociate into their fermionic constituents.

A prime motivation for the current experiments, however, is the desire to make atoms team up not as molecules--two tightly bound fermions--but as Cooper pairs--fermions that are loosely correlated in momentum space. The paired fermions would resemble the electron pairs in a Bardeen-Cooper-Schrieffer superconductor. Because such fermion pairs are a composite boson, they can occupy a common ground state and hence become a superfluid.

There would be no hope of seeing such a superfluid, however, unless it existed at temperatures accessible by the experiments. For these experiments, the gases are typically cooled to a few tenths of the thermal temperature T_F corresponding to the Fermi energy (Typically, T_F ≈ 1 μK.)

Fortunately, theorists have predicted that a novel superfluid phase might, indeed, exist at such temperatures--provided the degenerate Fermi gas is in the regime where interatomic forces are strong and attractive.¹

Happily, atomic researchers can control the sign and strength of such interatomic forces by applying a magnetic field. A number of current experiments are in the right regime to form a superfluid; the experimental challenge now is to prove that it's there.

Tuning the magnetic force to a particular strength may create Cooper pairs; tuning it to a different field value may promote the formation of molecules. The magnetic field thus becomes a powerful control knob, allowing researchers to explore the behavior of atomic gases as a function of the interaction forces. Many researchers dream one day of taking a system of particles smoothly from a molecular BEC to a BCS-type superfluid.

There's another reason for interest in the current experiments on degenerate Fermi gases: Ultracold, low-density atomic gases provide a useful environment to probe and control quantum phenomena. They offer a way to explore, in a tabletop experiment, the universal behavior of systems of strongly interacting particles. Theorists expect--and experimenters are beginning to show--that, in the strong-interaction region, the behavior of the atoms becomes universal, or independent of the details of the atomic potential.^2,3 Theorist Jason Ho of Ohio State University notes that studies in the region of strong interactions, where perturbation approximations no longer hold, should shed light on some of the most intractable problems in a variety of fields.

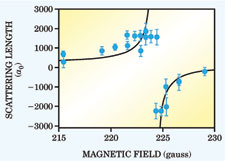
The applied magnetic field is able to control the sign and size of the interatomic forces through its impact on a parameter known as the S-wave scattering length, a. When a is much less than the interparticle spacing, the scattering cross section varies as a² and the mean-field interaction energy goes as na, where n is the density of atoms. (The mean-field energy is the average potential energy felt by one atom due to the presence of all the other atoms in the gas.)

Figure 1

For most values of magnetic field, a is small and relatively independent of the magnetic field. For certain values, however, the magnetic field causes the collisional energy between two atoms to approach the energy of a quasibound molecular state. At those values, known as Feshbach resonances, the interaction is greatly intensified and a diverges, as seen in figure 1. On one side of the resonance, a is positive, which signals a repulsive force between atoms; on the other side, it's negative and the force is attractive. Tuning the magnetic field knob through this region can thus bring about dramatic changes in the behavior of the gas.

When a exceeds the interatomic spacing, it's no longer valid to express the cross section or the mean-field energy in terms of a. Doing so would cause those quantities to grow without limit, in violation of the unitarity principle, which imposes a limit on the S-wave scattering cross section. Instead, the mean-field energy approaches a constant fraction of the Fermi energy. Without the dependence on a, the only length scale in the problem is the interparticle spacing, and the behavior should be universal for all strongly interacting particles.

Also in the region of large a, many-body effects become important, and the system behavior can no longer be described as the sum of interactions between pairs of atoms. A number of theorists from different fields have suggested that, in the unitarity limit, such many-body correlations result in an effective attractive interaction.

Several recent experiments performed on degenerate Fermi gases near Feshbach resonances have seen some of the effects predicted for large a. John Thomas and his coworkers at Duke University saw a hint of universal interaction in the expansion of a degenerate Fermi gas of lithium-6 atoms.⁴ Cindy Regal and Deborah Jin of the JILA-NIST-Colorado team in Boulder saw saturation effects in their measurements of the mean-field energy in a potassium-40 gas.⁵ Christophe Salomon of the Ecole Normale Supérieure in Paris (ENS) and his collaborators from the ENS, the FOM Institute in Amsterdam, and the Kurchatov Institute in Moscow found evidence that the interaction in their ⁶Li gas remains finite and attractive throughout the resonance region.⁶ That finding was echoed by data from Wolfgang Ketterle and his team from MIT.⁷

Ketterle says that, although in hindsight one can make a case for the breakdown of the scattering-length picture, he was completely surprised to see such strong interactions without strong losses by inelastic collisions. "I never thought that we would so soon be in a regime where we need new many-body theory."

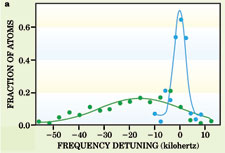
To detect the saturation of the mean-field energy in their degenerate Fermi gases, the Boulder and MIT teams introduced a new experimental technique: radio-frequency spectroscopy. That technique was used in a two-component Fermi gas--that is, a mixture of atoms with two different Zeeman spin states. For example, all the ⁴⁰K atoms in the Fermi gas used by Jin and her Boulder colleagues have total atomic spin of f = 9/2, but each atom can be in a different Zeeman spin state, described by the quantum number m_f. The Boulder group selects a mixture of two spin states, such as m_f = -9/2 and m_f = -7/2.

With an RF pulse, one can transfer atoms between the two spin states, and the transition is detected as a narrow spectral line. The presence of atoms in a third spin state, however, can slightly change the energy difference between the original two spin states, shifting and broadening the RF transition between them. This effect is illustrated in figure 2a, from the experiment by Ketterle and his MIT group. The observed change in frequency is a measure of the system's mean-field energy.

Figure 2

Figure 2b is a plot of the frequency shifts as a function of magnetic field. They are compared to a curve predicted by the theory of dilute atomic gases. Away from the Feshbach resonance, the data points line up along the curve. Within the resonance region, though, the measured shifts are much smaller than theory predicts. Regal and Jin obtained a similar result.

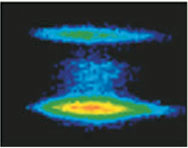
For several years, experimental groups have used various techniques to coax ultracold atoms to pair as molecules (see Physics Today, September 2000, page 46). Until recently, most efforts began with bosonic atoms, some within BECs. Now, there's great interest in forming molecules from fermions. In the process, atoms would move away from the governance by Fermi statistics to the rule of Bose statistics.

Regal, Jin, Christopher Ticknor, and John Bohn, all of the Boulder group, reported in July that they had formed molecules from atoms in two differing spin states.⁸ The researchers started with a degenerate ⁴⁰K Fermi gas, consisting of atoms in the m_f = -9/2 and m_f = -5/2 states. They held these atoms at a magnetic field just above the Feshbach resonance, where the interactions are attractive. For this system, molecule formation is expected on the other side of the Feshbach resonance. The experimenters ramped down adiabatically through the resonance region until, about mid-resonance, they saw a sudden decrease in the number of atoms. This dip could mean that the atoms have entered molecules, but it might also mean that atoms have simply been lost from the trap.

To see if molecules had actually formed, Regal and her coworkers probed with an RF pulse. The frequency was set so that any molecule that might have formed would dissociate into m_f = -9/2 and m_f = -7/2 atoms. The presence of spin m_f = -7/2 atoms, which were not initially present, was thus the signal that molecules had been formed. As seen in figure 3, such spin states did appear.

Figure 3

Since the Boulder paper appeared, a Rice University group⁹ and the ENS-FOM-Kurchatov collaboration¹⁰ have reported forming molecules from degenerate Fermi gases, and a team at the University of Innsbruck has described molecule production from an ultracold (but not degenerate) Fermi gas.¹¹ All three cite evidence that the molecules live for times on the order of at least one second, compared to lifetimes of milliseconds reported by the Boulder group. The longer lifetime means that the molecules can stick around long enough to form a BEC. Jin said that she and her coworkers are finding that the lifetime depends strongly on the magnetic field; they too are now getting lifetimes approaching those in the other expriments. The experimental groups report conversion efficiencies--percentages of atoms that enter molecules--that range from 50 to 80%.

In the Rice experiment, Randall Hulet and his colleagues formed molecules from a degenerate Fermi gas of ⁶Li atoms. Like the Boulder group, they ramped the magnetic field through a Feshbach resonance. To confirm formation of molecules, the researchers reversed the magnetic field ramp to return to the starting point; the missing atoms resurfaced as the molecules dissociated. In the ENS-FOM-Kurchatov experiment, Salomon and his collaborators, also working with a degenerate ⁶Li gas, were able to count the number of atoms that had not been bound in a molecular state; they also showed that the atom-to-molecule process is reversible.¹⁰

The Innsbruck group, headed by Rudi Grimm, conducted its experiment above the temperature where a degenerate Fermi gas forms, and the field was changed quickly rather than adiabatically. In contrast to the other experiments, the molecules in the Innsbruck case were formed by three-body collisions. The research team used a magnetic field gradient, as in a Stern-Gerlach experiment, to separate the atoms from molecules. The lifetime of the molecules was longer, perhaps because of the lower atomic density.

In their explorations of the strong-interaction regime, Thomas and his Duke colleagues found that their cloud of ultracold ⁶Li atoms, after its release from the trap, expanded rapidly in the transverse direction and very little in the axial direction.⁴ Such anisotropic expansion is a possible indication of superfluid hydrodynamics, which is collisionless. However, it can also be a sign of collisional hydrodynamics within the atomic cloud, as the Duke team and others have pointed out.

Superfluidity in a Fermi gas may reveal itself only through subtle signals. For all we know, several of the ongoing experiments may already have formed a superfluid. But how can it be detected? Hulet suggests that proving the presence of superfluidity may take several pieces of evidence--perhaps the observation of a superconductivity-like energy gap plus the sighting of resistance-free flow.

At the European Laboratory for Nonlinear Spectroscopy at the University of Florence, Massimo Inguscio and his colleagues are following a different strategy to reach fermionic superfluidity. They plan to use bosons as the glue for fermions, much as bosonic phonons help to couple the electrons in BCS superconductors. Inguscio's group has found that a mixture of potassium-40 atoms (fermions) and rubidium-87 atoms (bosons) has a naturally strong and attractive interspecies interaction, which should favor the pairing of fermions even in the absence of an external magnetic field.¹² The researchers also note that they can further increase the natural interspecies interaction by using a magnetic field to approach a Feshbach resonance.¹³ "We are also taking that approach," says team member Giovanni Modugno, "to try to form a heteronuclear molecule, which should have a permanent electric dipole moment."

No doubt all the experimental groups are now planning how to conduct the hunt for a superfluid. They have caught a whiff of their prey and are on its trail. In the meantime, they are enjoying the hunt.

2003 American Institute of Physics