

For this asignment, make your point2D store the coordinates as doubles, not ints.
You will need to define a data structure to encode a kd-tree such as below --- feel free to refine as needed.
typedef struct _treeNode {
point2D p; /* If this is a leaf node, p represents the point stored in this leaf.
If this is not a leaf node, p represents the horizontal or vertical line
stored in this node. For a vertical line, p.y is
ignored. For a horizontal line, p.x is ignored
*/
char type; / * this can be 'h' (horizontal) or 'v' (vertical), or 'l' (leaf)
depending whether the node splits with a horizontal line or vertical line.
Technically this should be an enum.
*/
treeNode *left, *right; /* left/below and right/above children. */
} treeNode;
typedef struct _kdtree{
treeNode* root;
int count; //number of nodes in the tree
int height; //height of tree
} kdtree;
In c++, it will look more like this:
class TreeNode {
private:
point2D* p;
char type;
TreeNode *left, *rigt;
public:
TreeNode(Point2D*);
~TreeNode();
};
class Kdtree {
private:
TreeNode* root;
int count ; //number of leaves in the tree
int height; //height of the tree
//build the kd-tree
TreeNode* buildKdtree(Point2D* sortedbyx, Point* sortedbyy, int n, int cuttype);
public:
Kdtree(Point2D* p, int n );
~Kdtree();
...
};
Note: Feel free to use Vectors instead of arrays everywhere.
You'll need to write the basic primitives for operating on a treeNode and on a kdtree, such as creating a node and creating an empty tree, printing a node, and printing a tree.
For example, include a function that prints some basic info about the kd-tree, such as number of nodes, and height. Call this function in the main functin so that we can see its output.
The function will take as argument an array of points and returns the kd-tree.
In C it might look like this:
/* Build a kd-tree for the set of n points, where each leaf cell contains 1 point. Return a pointer to the root. */ kdtree* buildkdtree(point2D* points, int n)In cpp write a constructor that looks like this:
public:
Kdtree(Point2D p[], int n );
Note: Since your coordinates are doubles and you generate the points randomly, its unlikely that you'll get coincident points in your set of points. If your coordinates are ints, you'll need to consider this issue. Below we assume that the points are distinct.
The generic constructor should first sort the points by Sort points by x-coord and by y-coord using system qsort.
point2D *points-by-x, *points-by-y; //allocate them, copy data from points then sort them
You need to use system qsort and define appropriate comparison functions. Points that have same x-coordinate or same y-coordinate can cause issues with the partition (for example...). To handle these cases elegantly think of using comparison functions that uniquely order the points:
//orders the points by x, and for same x in y-order
int leftToRightCmp(Point2D a, Point2D* b) {
...
}
//orders the points by y, and for same y in x-order
int bottomToTopCmp(Point2D a, Point2D* b) {
...
}
After sorting the points, the function shoudl call a helper function that takes more arguments and is recursive. In C it may look like this:
treeNode* kdtree_build_rec(point2D* points-sorted-by-x, point2D* points-sorted-by-y, int n, ...)In cpp it may look like this:
TreeNode* Kdtree::buildKdtree(Point2D* points-sortedbyx, Point* points-sortedbyy, int n, int cuttype);This helper function should build the kd-tree recursively. It should probably take the depth of the current node as a parameter and use it to decide whether to split vertically or horizontally.
The main challenge in this function will be make sure the recursion stops.
Stop the recursion when the node contains 1 point (and possibly earlier if necessary, depending on how you handle degenerate cases).
The median is the value in the middle index of the sorted array (sorted by x or by y, depending on the type of node). One way to set up the recursive calls is to put all points with x-coord smaller or equal to the median to the left, and the others on the right. Think of what happens when you have points with same coordinates, for example consider the case of points on the same vertical line. All x-coordinates are the same, and if you distribute all the points with x-coord smaller or equal to the median to the left, all points end up on the left side. You need to think if its possible to generate infinite recursion.
For e.g. consider the points (2,6), (3,6), (3,5) examined in the x-coordinate. Middle point is (3,6). But the third's point x-value is also 3, so it will go on the left side. Thus this passes the entire array to the next level. Then we examine them in the y-coordinate: (3,5), (3,6), (2,6) Middle point is (3,6). But the third point has same y-coord as the median, which means it will also go on the left side. Thus this passes entire array to next level again, i.e. infinite recursion. These points are not coincident but are collinear in just the wrong way to cause infinite recursion.
There are other ways to handle this, but an elegent way is to use the leftToRightCmp() instead of just comparing by x. In leftToRight order, no two points are equal (unless there are duplicate points, which we assume there aren't). All points before the median are strictly smaller than the median in leftToRight order. Put differently, a point p goes to the left of the median if p is smaller than the median in leftToRight() order, and goes to the right of the median otherwise. This way points are distributed evenly left and right and there is no infinite loop. It all works simply, when using the right comparator.
P1-sorted-by-x, P1-sorted-by-y P2-sorted-by-x, P2-sorted-by-y(you know their sizes), then do a pass through points-sorted-by-x and points-sorted-by-y and put them on the correct side.
if leftToRight(p, median) == -1: p goes to P1 else p goes to P2
In case you allocate the arrays (as opposed to using Vectors): Don't forget to free the arrays that you are done with, as there is no garbage collection in c/cpp.
Once it works on small inputs, run on sets of random points with values for various n. Make it so that when you press the space bar you get a different set of random points.
Teams shoud generate special initializers and everyone should include everyone's test cases in their code.
This means you shoud probably store regions in nodes.
The input points are generated in the range [0,WINDOWSIZE] x [0, WINDOWSIZE]. This is the region fo the root.
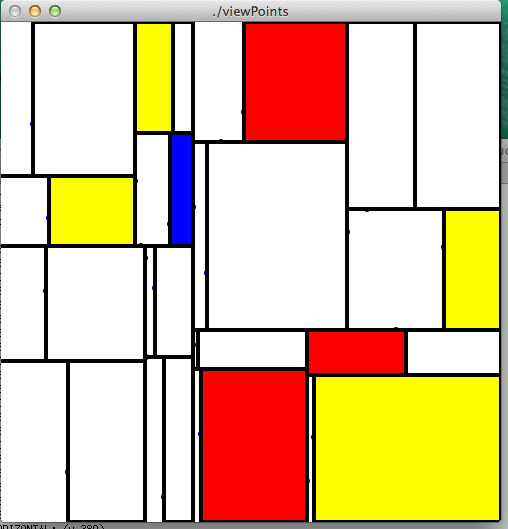
Render your kd-tree so that it looks similar to a Mondrian painting:


