Assignment: Motion planning with the Visibility Graph (VG)

One of the fundamental problems in robotics is motion planning: given a robot R and an environment (or physical space), a start position p_start and an end position p_end, find a path so that the robot can move from start to end, without collisisons.

Sometimes, depending on the problem, we might want the shortest path from p_start to p_end; other times just a path (not necessarily the shortest) may be sufficient.

General motion planning is quite difficult. We'll make some simplifying assumptions:

We'll look at the 2-dimensional motion planning problem: we'll assume that the environment consists of a set of 2D polygons that represent the obstacles; and the robot is a 2D-polygon (convex or not) and does not have joints (i.e. not an articulated robot).
We'll assume that the environment is static (the obstacles are fixed).
The environment is known, i.e. the robot knows the list of obstacles with their vertices and edges. That is, the robot does not rely on sensors to learn the environment, instead the environments is given.

Notation: we'll assume that the obstacles consist of n edges. So for us O(n) represents the complexiy of the obstacles (vertices plus edges). We assume that the robot is moving in a large bounding box B that contains all polygons.

Motion planning with roadmaps

The general idea of motion planning is to start by computing a decomposition of the free space (the space where the robot can move) into cells, and construct a road map of the free space to guide the motion between neighboring cells. The road map is essentially a graph of free space. Ideally we want to build the roadmap so that so that:

Any path in the road map corresponds to a collision-free path in the free space.
Any path in the free-space corresponds to a path in the road map.

If we are able to compute a road map of free space with these properties, then to move from s to t, we find a path in the road map from s to t. We know that any path in the road map is colision-free (by (1)), and we know that if a path in the road map does not exist, then no path exists (by (2)). Essentially we have reduced the motion planning problem to a path problem in a graph.

A point robot moving among polygonal obstacles in 2D

The simplest type of robot is that of a point robot, so we'll start by considering a point robot moving among polygonal obstacles.

Roadmap via trapezoidal decomposition: The free space can be decomposed as follows: from each vertex, shoot a vertical ray above and below, until it intersects with an edge (or the bounding box B). This is called a trapezoidal decomposition, and we have seen something very similar when we talked about polygon triangulation; in this case we have a set of polygons, not just one, but the idea is the same. This trapezoidal decomposition can be computed using standard techniques. Each trapezoid corresponds to a region of the free space. To guide movement between adjacent trapezoids, we can construct a road map as follows: we place one node in the center of each trapezoid, and we place one node in the middle of each vertical edge. There is an arc between two nodes if and only iff one node is in the center of a trapezoid and the other node is on the boundary of that same trapezoid. The figure below illustrates this (from 4M book). A path from start to end can be found via BFS in the road map. It can be shown that the road map has linear complexity O(n), which is good. But, paths obtained with this approach are not necessarily shortest. In summary, the roadmap idea is a useful thing to remember in general, but in the simple case of a point robot moving in 2D, we can do better.

The visibility graph: A different type of road map that can be used for finding shortest paths is the visibility graph: this is a graph whose vertices are the vertices of the obstacles, and its edges (u,v) are all the pair of vertices that can "see" each other, that is, segment uv does not intersect the interior of any obstacle. Below is a screenshot from http://www.cs.cmu.edu/afs/cs.cmu.edu/academic/class/16311/www/s06/lecture/lec8.html.

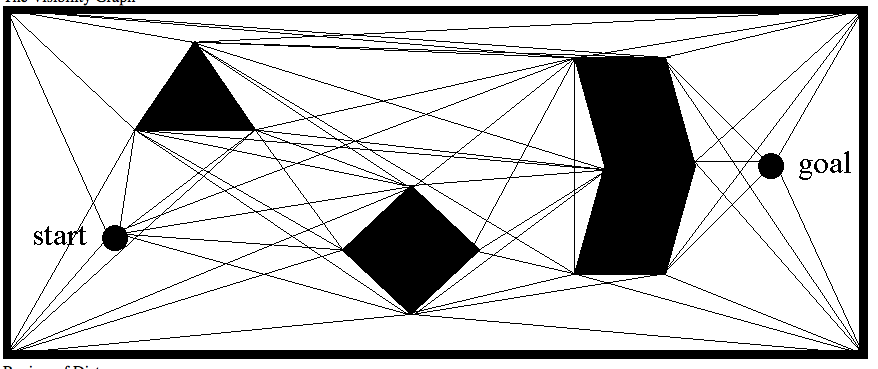
In class we'll talk about this in more details, and show that shortest paths in 2D have the very nice and convenient property that they are srtaight lines, and they have to go through the vertices of the obstacles. This basically means that any shortest path will be contained in the VG. Once the visibility graph (VG) is computed, the shortest paths from start to end can be computed for e.g. using Dijkstra's algorithm.

The problem with the VG approach is that the VG may have quadratic complexity in the worst case, and any approach that computes the whole VG is doomed to quadratic complexity. It would be nice to compute the shortest path from s to t on the fly, without using at least quadratic time and space to compute and store the VG. More on that later.

This assignment: Motion planning via VG for a point robot moving among polygonal obstacles in 2D

Generate a scene consisting of multiple polygonal obstacles and a start and end position. Have a pre-set scene, but also allow the user to enter the obstacles by clicking the mouse.
Compute and render the visibility graph.
Run Dijkstra's algorithm on the VG and render the resulting path (in a different color).

How to turn in: Please use the svn folder for the class, I will access the code there.

Enjoy!