Building a 2d-tree

In this assignment the goal is to build and visualize a two-dimensional kd-tree for a set of points in the plane. To manage complexity we'll split it in two parts:
  1. Part 1: build the kd-tree.
  2. Part 2: render/visualize the kd-tree, and make it look like a Mondrian painting.

Representing the kd-tree

For this asignment, make your point2D store the coordinates as doubles, not ints.

You will need to define a data structure to encode a kd-tree such as below --- feel free to refine as needed. 

typedef struct _treeNode treeNode;

struct _treeNode {
     point2D p; /* If this is a leaf node,  p represents the point stored in this leaf. 
                  If this is not a leaf node,  p represents the horizontal or vertical line
                  stored in this node. For a vertical line, p.y is
                  ignored. For a horizontal line, p.x is ignored
                */
     char type; / * this can be 'h' (horizontal) or 'v' (vertical), or 'l' (leaf)
                    depending whether the node splits with a horizontal line or  vertical line.
                    Technically this should be an enum.
                */
     treeNode  *left, *right; /* left/below and right/above children. */
}

typedef struct _kdtree{
   treeNode* root; 

   int count; //number of nodes  in the tree

   int height; //height of tree
} kdtree;
In c++, it will look more like this: 
class TreeNode {
  private: 
     point2D* p; 
     char type; 
     TreeNode *left, *rigt; 
  public: 
     TreeNode(Point2D*); 
     ~TreeNode();
};
class Kdtree {
  private: 
     TreeNode* root; 
     Kdtree* buildKdtree(Point2D* sortedbyx, Point* sortedbyy, int n, int cuttype); 

  public:
     Kdtree(Point2D p[], int n );
     ~Kdtree();
     ...
};

You'll need to write the basic primitives for operating on a treeNode and on a kdtree, such as creating a node and creating an empty tree, printing a node, and printing a tree.

For example, include a function that prints some basic info about the kd-tree, such as number of nodes, and height. Call this function in the main functin so that we can see its output.

Building a kd-tree

The function will take as argument an array of points and returns the kd-tree.

In C it might look like this: 

/* Build a kd-tree for the set of n points, where each leaf cell
   contains  1 point. 
   Return a pointer to the root.
*/
kdtree*  kdtree(point2D* points, int n)
In cpp write a constructor that looks like this: 
  public:
     Kdtree(Point2D p[], int n );

Note: Since your coordinates are doubles and you generate the points randomly, its unlikely that you'll get coincident points in your set of points. If your coordinates are ints, you'll need to consider this issue. From now on we'll assume that the points are distinct.

The generic constructor should first sort the points by Sort points by x-coord and by y-coord using system qsort. 

point2D *points-by-x, *points-by-y; 
//allocate them, copy data from points then sort them

You need to use system qsort and define appropriate comparison functions. Points that have same x-coordinate or same y-coordinate can cause issues with the partition (for example...). To handle these cases elegantly think of using comparison functions that uniquely order the points: 

//orders the points by x, and for same x in y-order
int leftToRightCmp(Point2D a, Point2D* b) {

}

//orders the points by y, and for same y in x-order
int bottomToTopCmp(Point2D a, Point2D* b) {

}

After sorting the points, the function shoudl call a helper function that takes more arguments and is recursive. In C it may look like this: 

treeNode* kdtree_build_rec(point2D* points-sorted-by-x, point2D* points-sorted-by-y, int n, ...)
In cpp it may look like this: 
TreeNode* Kdtree::buildKdtree(Point2D* points-sortedbyx, Point* points-sortedbyy, int n, int cuttype);
This helper function should build the kd-tree recursively. It should probably take the depth of the current node as a parameter and use it to decide whether to split vertically or horizontally.

The median and degenerate cases

The main challenge in this function will be make sure the recursion qstops.

Stop the recursion when the node contains 1 point (and possibly earlier if necessary, depending on how you handle degenerate cases).

The median is the value in the middle index of the sorted array (sorted by x or by y, depending on the type of node). One way to set up the recursive calls is to put all points with x-coord smaller or equal to the median to the left, and the others on the right. Think of what happens when you have points with same coordinates, for example consider the case of points on the same vertical line. All x-coordinates are the same, and if you distribute all the points with x-coord smaller or equal to the median to the left, all points end up on the left side. You need to think if its possible to generate infinite recursion.

For e.g. consider the points (2,6), (3,6), (3,5) examined in the x-coordinate. Middle point is (3,6). But the third's point x-value is also 3, so it will go on the left side. Thus this passes the entire array to the next level. Then we examine them in the y-coordinate: (3,5), (3,6), (2,6) Middle point is (3,6). But the third point has same y-coord as the median, which means it will also go on the left side. Thus this passes entire array to next level again, i.e. infinite recursion. These points are not coincident but are collinear in just the wrong way to cause infinite recursion.

There are other ways to handle this, but a very elegent way is to use the leftToRightCmp() and bottomToTopCmp(). These comparators uniquely order points by comparing both on x- and y-coordinates, and unless there are coincident points, no two points are equal under these compare functions. All points before the median are strictly smaller than the median, so they all go to the left; same for the points after the median. There is no need to handle degenerate cases, because under these compare functions there are none: all points are unique.

Maintaining points-by-x and points-by-y through the recursive calls

Allocate the sorted arrays for the recursive calls 
P1-sorted-by-x, P1-sorted-by-y
P2-sorted-by-x, P2-sorted-by-y
(you know their sizes), then do a pass through points-sorted-by-x and points-sorted-by-y and put them on the right side.

Don't forget to free the arrays that you are done with (ain't no garbage collection in c/cpp).

Testing

It goes without saying that you need to throroughly test your code. The goal of testing is to find bugs. Try to break your code. Once you find a bug, try to reproduce it on the smallest possible input ---- it's no fun debugging on an input of half a million points.

Once it works on small inputs, run on sets of random points with values for various n. Make it so that when you press the space bar you get a different set of random points.

Every team, please email your special test_cases to the whole class, so that everyone can include everyone's test cases in their code, and check that your code code works well in all cases.

Part 2: Rendering the kd-tree

Write a function that renders the kd-tree in OpenGL. Use the code for the previous assignments. The OpenGL part is pretty easy --- basically 
//for each node in the tree in some order {

      glBegin(gl_LINE);
      //identify the endpoints p1 and p2 of the line segment that you
      //need to draw
      glVertex2f(p1);
      glVertex2f(p2); 
      glEnd(gl_LINE);
}
The harder part in the rendering is identifying the endpoints of the line segment for that node. Note that the line x=x1through the root is infinite in the y-direction. The lines in the nodes left and right of the root are infinite on one side, and bounded by x=x1 on the other side. And so on. The region corresponding to a node (and thus the endpoints of the segments that will split it) can be computed based on the ancestors of the node in the tree.

The input points are generated in the range [0,WINDOWSIZE] x [0, WINDOWSIZE]. Thus a value of infinity in x or y direction should be set to WINDOWSIZE.

The rectangular region of each node in the kd-tree can be kept explictly, or can be computed on teh fly. It's your choice.

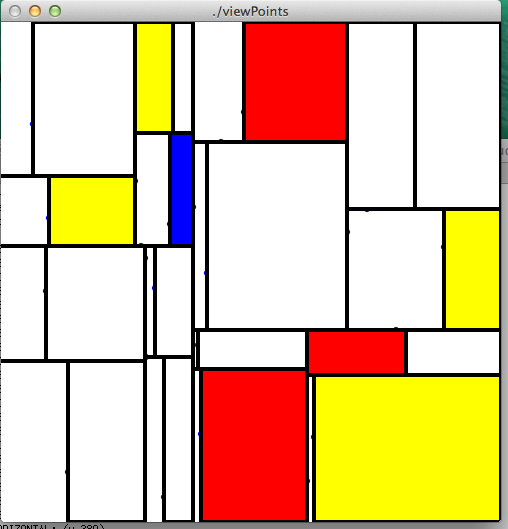
Render your kd-tree so that it looks similar to a Mondrian painting:

Submitting your work

Make a folder called kdtree in your svn folder on microwave. I will have access to this svn, so no need to submit anything --- just make sure everything is checked in.

Enjoy!