One of the fundamental problems in robotics is motion planning: given a robot R and an environment (or physical space), a start and end position pstart and pend, find a path so that the robot can move from start to end, without collisisons.
Sometimes, depending on the problem, we might want the shortest path from pstart to pend, other times just a path (not necessarily the shortest) may be sufficient.
The general motion planning problem is quite difficult. We'll make some simplifying assumptions:
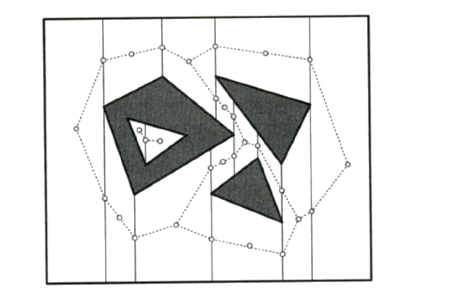
The simplest example is that of a point robot moving among polygonal obstacles. The free space can be decomposed as follows: from each vertex, shoot a vertical ray above and below, until it intersects with an edge (or the bounding box B). This is called a trapezoidal decomposition, and we have seen something very similar when we talked about polygon triangulation (here we have a set of polygons, not just one). This trapezoidal decomposition can be computed using standard techniques. Each trapezoid corresponds to a region of the free space. To guide movement between adjacent trapezoids, we can construct a road map as follows: we place one node in the center of each trapezoid, and we place one node in the middle of each vertical edge. There is an arc between two nodes if and only iff one node is in the center of a trapezoid and the other node is on the boundary of that same trapezoid. The figure below illustrates this (from 4M book). A path from start to end can be found via BFS in the road map. It can be shown that the road map has linear complexity O(n), which is good. But, paths obtained with this approach are not necessarily shortest.


In summary, the roadmap idea is a useful thing to remember, but in this simple case of a point robot moving in 2D, we can do better.
A different type of road map that can be used for finding shortest paths is the visibility graph: this is a graph whose vertices are the vertices of the obstacles, and its edges (u,v) are all the pair of vertices that can "see" each other, that is, segment uv does not intersect the interior of any obstacle. Below is a screenshot from http://www.cs.cmu.edu/afs/cs.cmu.edu/academic/class/16311/www/s06/lecture/lec8.html.
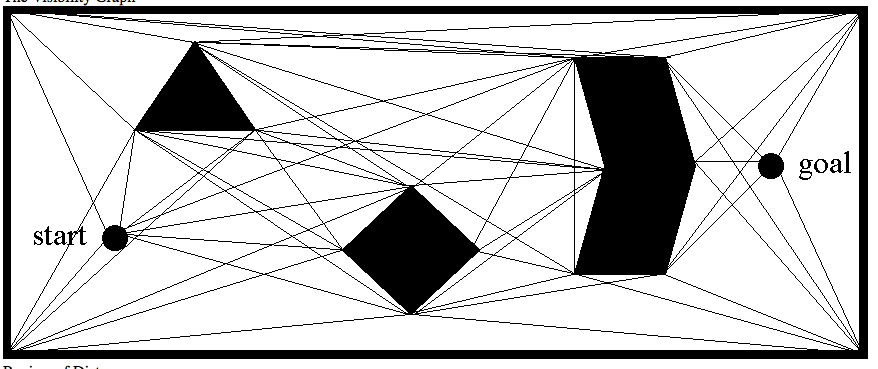
In class we'll talk about this in more details, and show that shortest paths in 2D have the very nice and convenient property that they are srtaight lines, and they have to go through the vertices of the obstacles. This basically means that any shortest path will be contained in the VG. Once the visibility graph (VG) is computed, the shortest paths from start to end can be computed for e.g. using Dijkstra's algorithm.
The problem with the VG approach is that the VG may have quadratic complexity in the worst case, and any approach that computes the whole VG is doomed to quadratic complexity.
How to turn in: Please use the svn folder for the class, I will access the code there.
Enjoy!