Assignment 3: Polygon triangulation

Several other ideas came up in class, all running in worst case quadratic time --- feel free to implement any of them instead of ear-removal-based one.

You can use as start point the code form previous assignments. You will need to write a function that takes a polygon as argument, and computes a triangulation.

It is up to you how you represent a triangulation: it can be simply as a list of edges, or a list of triangles.

Any triangulation of a polygon with n points will have precisely n-2 triangles.

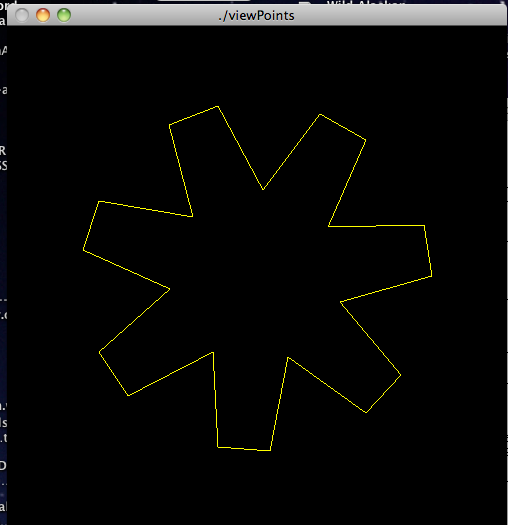
To test your triangulation, you will have to create some test polygons, either by hand (listing the vertices), or in an automatic way. I created some in viewPoints.c that generate polygons like this:

To compile it and run it grab the whole directory here (the other files are not changed).

In this code I represented the polygon as an array of vertices ---- if your representation is different, feel free to update the code to suit yours. Basically your code needs to have some way to generate some test polygons --- either you create your own or you use mine.

Either way, you will need to update viewpoints.c to draw the triangulation. Precisely what you need to do depends on how you store the triangulation:

• if you store it as a list of edges: you'll need to loop through the edges something like this:

    for each edge {
        gl_begin(GL_LINE)
        glVertex2f(...); //first vertex
        glVertex2f(...); //second vertex
        gl_end(GL_LINE)
    }
    

• if you store it as a list of triangles: you'll need to loop through the triangles and use

    for each triangle {
        gl_begin(GL_POLYGON)
        glVertex2f(...); //first vertex
        glVertex2f(...); //second vertex
        glVertex2f(...); //third vertex
        gl_end(GL_POLYGON)
    }
    

  ---

  Last modified: Wed Mar 5 17:16:43 EST 2014