Develop C/C++ code to render a grid terrain using OpenGL in a 2D top-down view (that is, using the default OpenGL viewpoint and projection). Your program will take the name of the input grid as an argument on the command line. The grid is assumed to be in ascii format.
Example:
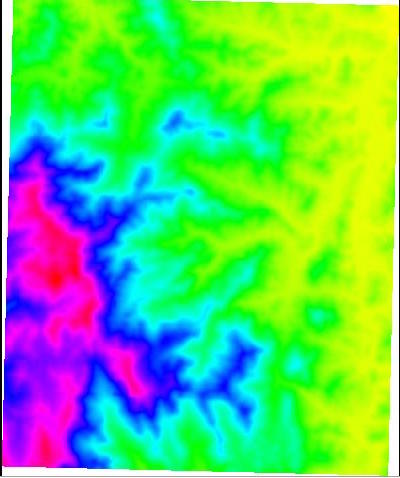
[ltoma@dover:\~] rendergrid ~/csci3225/DEM/set1.ascWill display something like this:

Implement at least two different color maps, and allow for an easy way to see them (ideas: cycle through them with a keypress).
Note: OpenGL 1.X is now deprecated and subsequent version have moved to shaders and vertex arrays. OpenGL 1.X is still perfectly fine for applications that do not need fancy features and it provides an easy way to get something up and running fast.
glBegin(GL_TRIANGLES); glVertex3f(...); //vertex1 glVertex3f(...); //vertex2 glVertex3f(...); //vertex3 glEnd();
When you specify a vertex, you will need to specify its coordinates (x,y,z). Note that the X and Y axis go to the left and up, as usual, while the rows and columns in the grid increase down and to the right. The origin (0,0) corresponds to point at row = nrows-1, and column=0. You'll need to think of this when you determine the x,y coordinates of point (i,j).
In this assignment you will render the grid in a top-down 2D view, which means essentially the the z-coordinate of the points does not matter. You can set z=0; or you can specify the z-value of the point (which you know from the grid) but OpenGL will ignore it in a 2D projection; however if you are careful with the z-values it will be very easy to switch to a 3D view.
However, you will need consider the elevation of points when determining the color of a point. To color a point p(i,j) at row i and column j, you will have to compute color(p) based on the elevation Z[i][j] of p (here I denoted the elevation grid by Z); let's assume that you write a function getColor(i,j) that returns the color of pont (i,j). Then you will use it to set the color for each vertex in a triangle. something like this:
glBegin(GL_TRIANGLES); glSetColor(getColor(vertex1)); glVertex3f(...); //vertex1 glSetColor(getColor(vertex2)); glVertex3f(...); //vertex2 glSetColor(getColor(vertex3)); glVertex3f(...); //vertex3 glEnd();
/*
assume that we computed the min and max elevation of the grid, and
initialized an array, say, float ElevRange[5] so that
ER[0]= min
ER[1] = min + (max-min)/5
ER[2]= min + 2*(max-min)/5
ER[3]= min + 3(max-min)/5
ER[4] = max
*/
getColor(i,j)
if Z[i][j] == NODATA return (color for NODATA)
If Z[i][j] between ER[0] and ER[1]: return (color for first bucket)
If Z[i][j] between ER[1] and ER[2]: return (color for second bucket)
If Z[i][j] between ER[2] and ER[3]: return (color for third bucket)
If Z[i][j] between ER[3] and ER[4]: return (color for fourth bucket)
The colors corresponding to each bucket shoudl be stored in an array
for example
float[3] Color[5]; //Note: not sure if this actually compiles, but basically each element //has to be a color, which is an array of 3 floats
OpenGL stores a color as a triplet (R, G, B), each color component is a float that can range from 0.0 to 1.0, where 0 is no color and 1 is full color.
For example,
glColor3f(1.0f, 0.0f, 0.0f);sets the color to RED.
Black corresponds to (0,0,0), and white corresponds to color (1,1,1). Setting all color components to be equal, like (c,c,c), for some value 0 <= c<= 1, gives gray shades from white (all compoenent 1) to black (all components 0.
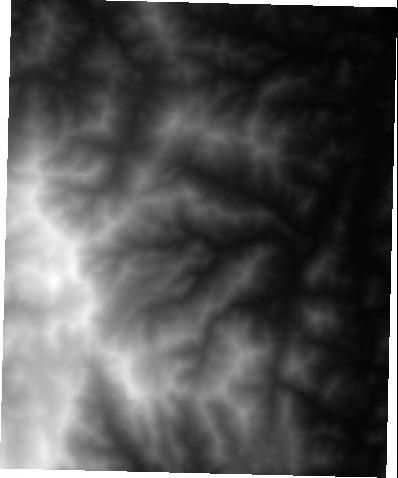
To get a continuous gray shade map, we can set all color components of point p(i,j) as a linear function of the height Z[i][j], being careful to map min to 0, and max to 1. For example:
int[3] getColor-gray (i,j)
if Z[i][j] == NODATA (return color for NODATA)
else int color[3];
color[0]=color[1]=color[2] =(Z[1][j] - min/ (max - min)
return color
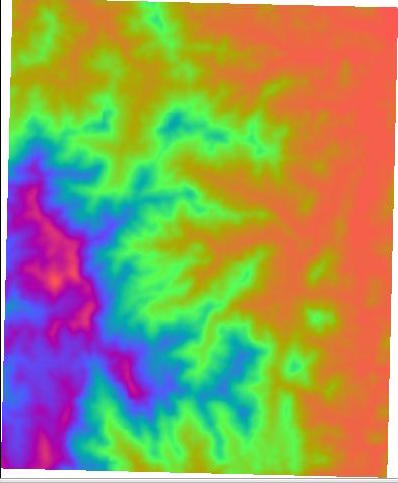
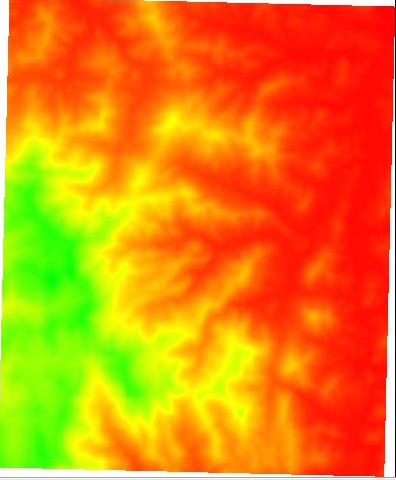
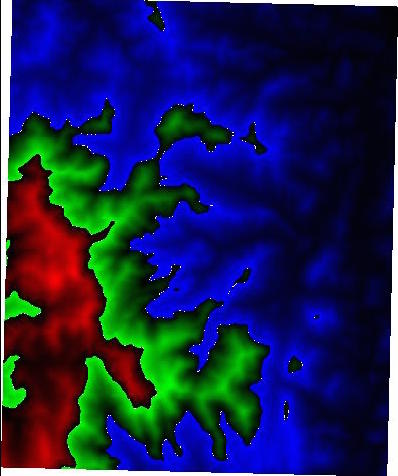
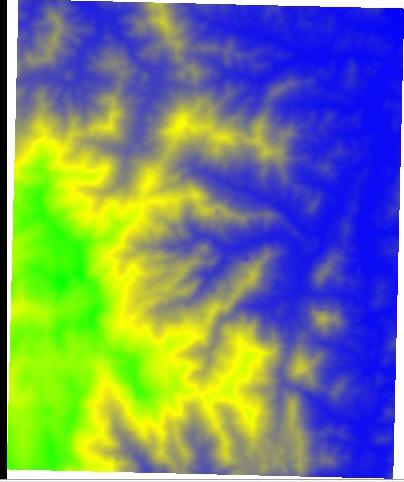
Now you want to extend your discrete color map so that, when the elevation of a point (i,j) falls in a certain elevation bucket, call it [h,h'], we want to smoothly interpolate the color of the point (i,j), function of its height, between the color correponding to h and the color corresponding to h'.
Let's say you divided the elevation range in 4 intervals bounded by 5 elevation boundary values stored in ER[0..4], and you have 5 colors Color[0..4]. For this part, we think of
Color[0] as corresponding to elevationER[0] Color[1] as corresponding to elevationER[1] ... Color[4] as corresponding to elevationER[4]
When a point (i,j) in some interval [h,h'], you want to interpolate its color smoothly based on the color C for h and the color C' for h'.
Our color C has 3 components, C' has 3 components, and the color of our point (i,j) will have 3 components. Let's think one color component at a time. Let's think of the Red.
The R of color C will be a value in [0,1], and the R of color C' will be a value in [0,1]. Let's call these R and R'. These values will be specified by you, probably hard-coded at the top of your code. The Red of point (i,j) has to interpolate smoothly between R and R', such that it is equal to R when Z[i][j] is precisely h, and it is equal to R' when Z[i][j] is precisely h'. Our abstract procedure is the following:
get-red (i,j) //assume Z[i][j] falls in interval [h,h'] //return a red value for point (i,j) // the red value is a smooth function such that: // if Z[i][j]=h: then the red value of this point must be the Red value // for the color specified for h // if Z[i][j]=h': then the red value of this point must be the Red value // for the color specified for h' //note: your function can be linear, but not necessary
There is a way to speed up the rendering by using what's called a triangle strip instead of a set of separate triangles. In a triangle strip, instead of specifying every single triangle, you specify a set of vertices p1, p2, p3, ... and GL draws the triangles for you assuming every 3 consecutive vertices form a triangle; to use this, you will have to specify your vertices in such an order that every 3 consecutive vertices form a triangle in the grid ---- if you chose to implement this, leave it for a second pass, once you got the simpler version (the one without triangle strip) to work.
When invoked with a wrong number of arguments your program should display a help message just like a standard unix command. Your program should correctly handle the situations when the input file does not exist and other common error scenarios.
Enjoy!