Csci 210: Tetris I

(Laura Toma adapted from Eric Chown based on a lab developed at Stanford by Nick Parlante)

Overview

In this lab you will start developing a Tetris game. The design will emphasize elemental Object Oriented Programming (OOP) design -- using encapsulation, to divide a big scary problem into many friendly little independently testable problems. In the first part of Tetris (this lab) you will set up the Piece class. In the second part (next lab) you will builds the Board class and some other fun bits. That will probably be more than enough, so I'll probably provide the last part for you.

For reasons that will become clear later, there is a theme of efficiency in this design. We are not just writing classes that implement Tetris. We are writing classes that implement Tetris quickly.

Background

You all know Tetris..

Piece

There are seven pieces in standard Tetris.

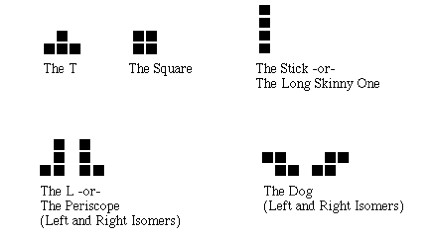
Each standard piece is composed of four blocks. The two "L" and "dog" pieces are mirror images of each other, but we'll just think of them as similar but distinct pieces.

A piece can be rotated 90 degrees counter-clockwise to yield another piece. Enough rotations get you back to the original piece--- for example rotating a dog twice brings you back to the original state. Essentially, each tetris piece belongs to a family of between one and four distinct rotations. The square has one, the dogs have two, and the L's have four. For example, here are the four rotations (going counter-clockwise) of the left hand L:

Our abstraction will be that a piece object represents a single Tetris piece in a single rotation, so the above diagram shows four different piece objects.

Body

A piece is represented by the coordinates of its blocks which are known as the body of the piece. Each Piece has its own little coordinate system with its (0,0) origin in the lower left hand corner of the rectangle that encloses the body. The coordinates of blocks in the body are relative to the origin of the piece. So, the four points of the square piece are then:

(0,0)  <= the lower left-hand block
(0,1)  <= the upper left-hand block     
(1,0)  <= the lower right-hand block        
(1,1)  <= the upper right-hand block

Notice that not all pieces will actually have a block at (0,0). For example, the body of the following rotation of the right dog:

has the body:

[(0,1),(0,2),(1,0),(1,1)]

A piece is completely defined by its body -- all its other qualities, such as its height and width, can be computed from the body. The above right dog was a width of 2 and height of 3. Another quality which turns out to be useful for playing Tetris quickly is the skirt of a piece.

Skirt

The skirt will be an int[] array, as long as the piece is wide, that stores the lowest y value for each x value in the piece coordinate system.

The skirt of this piece is {1, 0}. We assume that pieces are not disconnected (do not have holes in them)---for every x in the piece coordinate system, there is at least one block in the piece for that x.

Rotations

The Piece class needs to provide a way for clients to access the various piece rotations. When a client has a particular piece (e.g. the right dog) and the player hits the rotate key, the client will need to immediately know what the piece will be when it is rotated. To accomplish this we will let the client ask each piece for the "next rotation." This will be accomplished by a method that returns a piece object that is simply the current object after rotation. This is an example of an "immutable" paradigm -- there is not a rotate() message that changes the receiver. Instead, the piece objects and their rotations are all created ahead of time and are read-only. The client is given the ability to iterate over them (the String class is another example of the immutable paradigm). This is a much faster solution than computing rotations on the fly.

For efficiency, we will pre-compute all the rotations just once such that a Piece will actually be a circular list of all of the rotations. Given a piece object, the client will be able to get the "next" piece by just retrieving the next item in the circular list. In essence, this allows the client to obtain each rotation in constant time. This strategy will be used on virtually all public methods over the course of this project. For example the skirt should be computed at piece creation time so that at runtime it is merely returned, not computed then returned.

It is worth making the last point again: all of the rotations, skirts, etc. are computed when the initial pieces are made. This is done exactly once. Once they are made then the Tetris game during its game play just accesses what already exists.

Piece.java code

The Piece.java starter files has a few simple things filled in and it includes the prototypes for the public methods you need to implement. Do not change the public prototypes ---- your Piece will need to fit in with the later components. You will want to add your own private helper methods which can have whatever prototypes you like. You can find this file (and all the others for this lab) here.

Rotation strategy

The overall piece rotation strategy uses a single, static array with the "first" rotation for each of the 7 pieces. In the code you can find this in the getPieces method which is already written for you. Each of the first pieces will become the first node in a little circular linked list of the rotations of that piece. The first node will be passed into the pieceRow method which is the key method you have to write for the first part of Tetris.

The player uses nextRotation() to iterate through all the rotations of a tetris piece. The array is allocated the first time the client calls getPieces() -- this trick is called "lazy evaluation" -- build the thing only when it's actually used. getPieces will set up the first Piece in the list and ask pieceRow to build the rest of the list. pieceRow will work by starting with the first Piece, rotating it to get a new Piece, linking that new Piece to the first Piece, and then repeating the process until the rotated Piece is equal to the new Piece (at that point you will have generated the entire list and need to make the list circulur).

The hard work in the program is figuring out how to start with an initial array of points and use them as a starting point to generate a circular list. Each item in the list will itself be a Piece (which means that you'll need to call the Piece constructor).

Rotation tactics

You will need to figure out an algorithm to do the actual rotation. Get a nice sharp pencil. Draw a piece and its rotation. Write out the coordinates of both bodies. Think about the transform that converts from a body to the rotated body. The transform uses reflections (flipping over) around various axes. Ask yourself how the height of the original is related to the width of the rotated Piece and vice versa.

Example: The right dog has body [(0,1),(0,2),(1,0),(1,1)]. After one rotation its body is [(1, 0),(0,0),(1,1),(2,1)]. After another rotation its body is back to the original.

Equals

Remember == normally only works with primitive types. You must determine how to tell if two pieces are equal (e.g. by looking at the individual blocks). This is absolutely crucial in making your piece class work correctly.

Private helpers

You will want private methods behind the scenes to compute the rotation of piece and assemble all the rotations into a list. Also notice that the computation of the width/height/skirt happens when making new pieces and when computing rotations -- don't have two copies of that code.

Generality

Our strategy uses a single Piece class to represent all the different pieces distinguished only by the different state in their body arrays. The code should be general enough to deal with body arrays of different sizes -- the constant 4 should not be used in any special way.

JPiece test

Each row in the PieceTester window below is an instance of JPieceTest. Each JPieceTest component takes a single piece, and draws all its rotations in a row. The code is provided for you so you can test your Piece code.

Here's how the JPieceTest works:

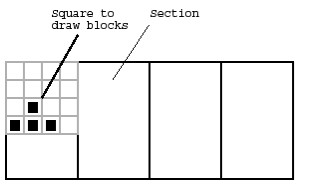
Divides the component into 4 sections. Draws each rotation in its own section from left to right, stopping when getting to the end of the distinct rotations.
Allows space for a square 4 blocks x 4 blocks at the upper-left of each section. Draws the blocks of the piece starting at the bottom of that square. The square won't fit the section exactly, since the section may be rectangular.
When drawing the blocks in the piece, leaves a one-pixel border not filled in around each block, so there's a little space around each block. Each block is drawn as a black square, except the blocks that are the skirt if of the piece -- they are drawn as yellow squares. Draws the blocks in yellow by bracketing it with
```
g.setColor(Color.yellow);
//draw block
...
g.setColor(Color.black);
```
At the bottom of the square, draws the width and height of the block with a string like "w:3 h:2". The string is red.

The last part of the JPieceTest class is a test main, to test your Piece class, that draws all the pieces in a window that looks like this: