Csci 210 Lab 10: Vizualizing Terrains

(Laura Toma)

Overview

Vast amounts of terrain data is available from remote sensing technolog. Terrain data can be used to model and understand a wealth of natural processes in geosciences, and beyond. In this final lab you will develop an application to display terrains.

Representing terrains

Terrains are represented by sampling points on the terrain and recording the geographical coordinates {x, y} of the point and the coresponding elevation {z} of the terrain at that point. Thus a terrain is represented as a cloud of points {x, y, z} stored in a file.

The most common terrain data available comes in form of a grid: this means that the points {x, y} are sampled uniformly with a grid. In a grid terrain the individual coordinates {x, y} of the points need not be specified. It is sufficient if we know the coordinates of the upper-left corner of the grid and the spacing between sample points. If these are specified, the geographical coordinates of the grid points are implicit.

A grid terrain consists of a header, and a set of points {z} that represent the elevation of the terrain sampled with a uniform grid. Here is a grid file, set1.asc, that represents a basin in the Sierra Nevada range in the south-west. Open it and take a good look at it.

The format of a grid file is standard. The first 6 lines in the file represent the header of the terrain; it stores the number of rows in the grid, the number of columns, the geographical coordinates of the lower left corner, the spacing in the grid (assumed to be the same both horizontally and vertically), and a nodata value (this is the value that is used for points where the elevation could not be measured).

ncols         391
nrows         472
xllcorner     271845
yllcorner     3875415
cellsize      30
NODATA_value  -9999

Following the header there are nrows lines, each line containing ncols values, for a total of nrows * ncols values. These values represent the elevations sampled from the terrain. Thus, a grid terrain is basically a 2D-array of elevation values. You can assume that the elevations are integers (though you can also use floats or doubles if you want). The dimensions of the grid can be found out from the header. The other information stored in the header (xllcorner, yllcorner, cellsize, NODATA_value) you will happily ignore for this lab since we won't care about geographical coordinates---- but you have to read them anyways in order to get to the point in the file where you can start reading the elevations.

Loading a terrain from file

Your program should take the name of the file on the command line. Let's say your program is named LTTerrainFlow. Then it should be run as follows:

 java LTTerrainFlow set1.asc

The first thing your program should do is open the file, read the header, create an elevation grid and load it with the values from the file. Encapsulate this code in a function

loadGridFromFile(String fileName)

The program should run with any grid file, and I will add a few more here.

Visualizing a terrain

Once the terrain is loaded in memory, the user should be able to vizualize it in 2D window. You can have a window pop up by default after you load the file, or you can have the user push a "Display Elevation" button in order to trigger the display. In either case, write a function that displays a grid passed ar argument

void displayGrid(int[][] grid)

It is better to make this function take a grid as an argument---you will use it to vizualize any grid, not only an elevation grid.

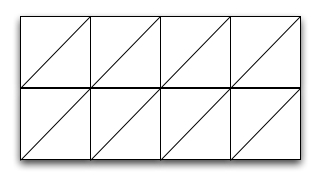
To display a grid you will draw a triangulation as below:

Each point (i, j, z) in the grid will be drawn on the window at position (i', j'), where (i,j) are the row and column in the grid (grid coordinates), and (i', j') are window coordinates. Note that we ignore true geographical coordinates, and we use (row, column) of the point--- we don't care about teh true geographical location anyways, at least, not for this lab. As you are trying to get things to work, you can make the assumption that the window coordinates are the same as the grid coordinates; For the test grid set1.asc this will work well, if you open a window of 500 by 500 pixels.

Scaling the grid to the window: A good program should scale the terrain to the window; assume a square window, for simplicity. When displayed, the longest side of a terrain should match the window dimension.

This can be done by computing two stretch factors, one horizontal and one vertical: stretch_horiz and stretch_vert. The intended usage is that you use

i' = i * stretch_horiz;
j'= j * stretch_vert;

The stretch factors can be computed knowing the size of the window, and the dimensions of the grid. You may need to change the lines above to account for centering, if you need to.

Colors

Note that so far you used only the (i, j) of each point, but not its elevation. You will use the elevation to choose the color of a point (or line).

In Java the color is specified as a triplet (r, g, b), where r, g, b are values in the range [0.0, 1.0] specifying the red, green and blue intensity in the color, respectively. 0.0 represents the darkest, and 1.0 the lightest. WHITE corresponds to (1.0, 1.0, 1.0) and BLACK corresponds to (0.0, 0.0, 0.0).

Remember that on a graphics object you can change the color using

Color c = new Color (r, g, b);
g.setColor(c);

In order to make the height reflect the elevation, you will have to come up with a formula to set r,g,b as function of the elevation; you will need to do this every time you call drawLine, to set the color of the line as a function of the elevation of that line. Assume that the elevation of the line is the average of the elevation of its points.

To come up with a logic for setting r, g, b, remember that r, g, b must be values in [0.0, 1.0], with 0.0 corresponding to highest elevation, and 1.0 to lowest elevation.

The easiest way would be to set all of them to the same value. Equal values for r,g and b give a gray color, so it will result in a gray-scale image.

r = g = b = ...
c = new Color(r, g, b);
g.setColor(c)

Interface, etc

Your program should have a window and one button --- to display the elevation grid. Keep it simple.

Encapsulate, use small functions, write nice code, write code incrementally and debug it before you move to the next step.

Have fun!