David Francis Website: AskANerd: Why does the moon rise earliest in the evening when full?

AskANerd: September 19, 2002

Bev Whittaker of South Africa (?) asks:

Two questions: 1. Why does the moon rise earliest in the evening when full? 2. Why does the time of total solar eclipse occur at the time of the new moon?

The Nerd responds: Bev, before I can answer your question I must make sure that by evening, you mean after sunset. Sometimes people think of evening as a specific time of day, such as 6pm, and if we think of evening that way, then your question isn't quite right. For example, the waning gibbous moon actually rises before the sun sets, and in the Summer months, that might be considered the evening. However, I think what you are asking is "Why does the full moon rise the earliest after dark (i.e., after sunset)."

The first thing we need to understand is what is going on that causes the different phases of the moon. I touched on this a bit in my When is the moon really full? response, but let's go into a bit more detail.

Many people believe the phases of the moon are caused by the moon slipping into the earth's shadow. In fact, the reason is much more simple. Everyone knows that the Earth is never completely illuminated by the Sun. Rather on half of the Earth is illuminated (daytime) while the other half is dark (nighttime). The same holds true for the moon. However, because the moon is circling the Earth, how much of this illuminated side of the moon we get to see depends on where the moon is.

To get the basic idea, get a ball and a flashlight. If you can wait until nighttime, you might to go outside where the light from the flashlight will have fewer objects off which to reflect. Now, hold the ball right in front of you at arm's length. Now with your other hand, turn on the flashlight and point it down your other arm towards the ball. You can now see one complete side of the ball lit up. Now, holding the ball in place, take your other arm (with the flashlight still pointing at the ball) and swing it around so that it is now directly to the left or right of the ball. Now how much of the ball can you see lit up by the flashlight? If you have a good, dark place to perform this experiment with enough open space so that the light doesn't reflect back to the other side, you should see that from your position you can only see a quarter of the ball illuminated. While 1/2 of the ball is still receiving light from the flashlight, the curvature of the ball allows you to only see 1/2 of that: that is, one quarter. Try a few other positions with the flashlight. You should see that you can mimic all the phases of the moon with your flashlight and tennis ball.

Figure 1

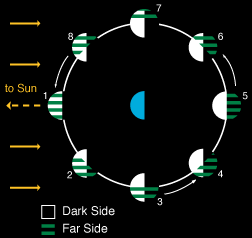
If you weren't able to perform that experiment, then let's look at a diagram of the sun, earth, and moon directly (Figure 1). I found this diagram on the NASA website. In this view, the sun remains constantly in the left of the picture, but the moon is moving about the earth in its orbit. The white portion of the moon shows the side that is being illuminated by the sun, but the green bars show the areas that, although illuminated, we can not see because of the moon's curvature. Pass your mouse over each phases to get a picture of what the phase looks like from earth

Now, look at the picture in figure 1 and imagine a clock face superimposed over the top of it. Hopefully, you can see that in order for the moon to be full, then with the Earth at the center, the sun must be a 9 o'clock and the moon at 3 o'clock. If the moon were in any other position, then it would be in a different phase. So, knowing now that this is so, take a look at Figure 2. (Don't be confused by the numbers on the picture. These represent the 8 phases of the moon, not the positions I am talking about. When I say 3 o'clock or 9 o'clock, I speaking in terms of directions. You have probably seen sailors and pilots use this kind of terminology on TV or in movies.)

Figure 2 is a view from space very similar to the one if Figure 1 except that in this case we are only interested showing the position of the sun and moon on the night of a full moon. Notice that the sun is at 9 o'clock and the moon is at 3 o'clock. Now take a look at the Earth in the middle. Imagine you are the person standing one the earth in that picture. Can you guess what time of day it is in that picture? Well, notice that the sun is directly above your head and that the moon is on the other side of the planet and cannot be seen. Given that scenario, I think we can safely surmise that it must be around noon. If you look at Figure 3, you will see what you would be viewing at this time, not from space, but from the ground.

Alright, here we are at noon on the day of a full moon. Let's move along to sunset to see what happens. Click the "Give it a turn" button one time to rotate the Earth 1/8 of a rotation.

Figure 2

Figure 3

Okay, now we have moved a few more hours towards sunset. Notice that the sun has begun to sink in the sky. This is apparent in Figure 3, but you can see this in Figure 2 as well. Notice how the sun has moved closer to the white line upon which you are standing. The white line here represents your viewing horizon from the ground. Give the button another click. Now we have sunset. And look, now that the sun is on one horizon, the moon begins to appear on the other horizon (in the east). This isn't surprising since they are exactly 180 degrees apart. Click the button again. Now the earth has spun into night. The sun has slipped below the horizon and the moon has risen well above it. Keep on clicking the button until you get sunrise and then keep on clicking until you get moonrise again. If you keep on clicking you will see that this process repeats over and over.

Of course, we know that this process doesn't repeat every night (there is only one full moon every month). This, of course, is because the sun and moon don't remain lined up at 9 o'clock and 3 o'clock every night. Because the moon revolves around the earth, in just a few nights, it will have moved to its last quarter when it will be at 12 o'clock high. Because of this movement, the moon will actually have already risen above the horizon before the sun has set. But only on the night of a full moon does the moon rise just as the sun is setting.

Now, on to question 2. Unlike the phases of the moon, eclipses are caused by shadows. Lunar eclipses are caused when the moon moves into the Earth's shadow, and the more spectacular solar eclipses occur when the Earth moves into the Moon's shadow.

Take a look at Figure 1 again. In which of these phases could the moon cast a shadow on the Earth? Certainly not during a full moon; the moon is on the wrong side of the Earth at that point. Take a look at Figure 4. The blue cones represent the shadows thrown by the Earth and Moon. At a full moon, the moon's shadow is pointed away from the Earth. So what is the only phase in which the moon could cast a shadow on the Earth? Clearly, it is when it is a New Moon--that is to say, when the moon is directly inbetween the Sun and Earth (Figure 5).

Having said that, a person might well wonder why doesn't every New Moon produce a solar eclipse?

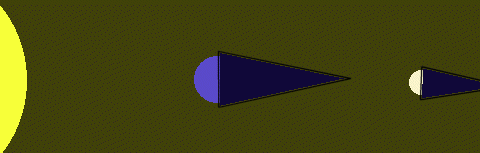Figure 4

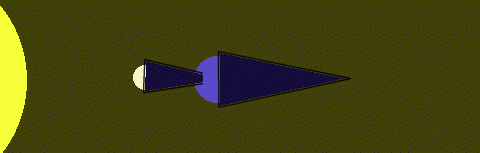Figure 5

Figure 6

The answer is that there is a lot more going on that my simple 2-D drawings don't show. The Earth and Moon are actually very far apart from each other and the slightest difference in their positions can mean that the Moon's shadow will not be cast on the surface of our planet. Figure 5 shows an eclipse occuring, but this is actually a rare and very localized effect. A far more common New Moon scenario looks like the one in Figure 6 in which the moon is too far from the Earth to have its shadow reach our planet.

Another interesting fact about solar eclipses is that it is only a coincidence that the moon and sun are of such sizes and distances from our planet that they appear to be about the same size to our view. The moons orbiting Mars, for instance, could never produce a total solar eclipse on that planet because they are simply too small to block out the sun.