To facilitate this design, new classes Grid and Cell have been designed with methods that enable the interaction to define a rectangular board, make plays on the board, examine the state of the board, and so forth. Part 1 is a brief tutorial on these classes.

These four objects should be familiar to you: a Button, a menu of Choices, a TextArea, and a TextField. These are designed to allow you to exercise the methods of the Grid and Cell classes.
A "cell" is a rectangle inside a grid that has one of four possible values - X, O, empty or filled - and one of several possible colors. The key public variables and methods for the class Cell are summarized as follows:
A "grid" is a square array of cells. The key public variables and methods for the class Grid are summarized as follows:
Grid (int rows, int cellSize, int offset); // number
or rows (and columns), size
// of a cell in pixels, and
offset from
// upper left-hand corner
of the frame
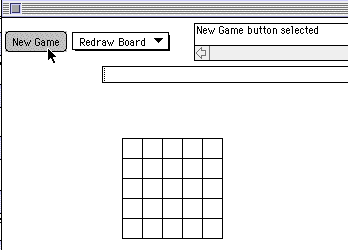
This display is achieved in the BoardGame program by declaring and initializing the variable named theBoard . The actionPerformed handler initializes this variable as a new Grid in response to a selection of the button "New Game":
b = new Grid(5, 15, 120);This statement calls for the creation of a 5x5 grid whose cells are 15 pixels in size, and which is displaced 120 pixels in both directions from the upper left-hand corner of the Frame. The rows and columns of this array are numbered from 0 to 4, reading vertically from the top and horizontally from the left.
Any cell in the grid may be set by a single mouse click, but only after a particular choice from the menu has been selected:
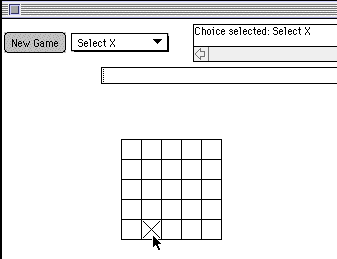
For example, select the choice "Select X" and then click the mouse in row 4, column 1. The program should give you the following response.
The itemStateChanged event handler for the choice "Select X" contains the following line of code, which sets the char variable current_player to EX (the phrase Cell.EX says that the constant EX is defined inside the Cell class):
if (current_choice.equals("Select X"))
current_player = Cell.EX;
The mouseClicked handler contains the following phrase, which
actually sets the designated square to X, but only if the x-y pixel coordinates
of the click are somewhere inside the boundaries of the grid b:
if (b.contains(last_x, last_y))The contains method call does two things: it determines whether or not the coordinates of the pixel at the point (last_x, last_y) are inside the grid, and if so it translates that point to a corresponding row and column number for that point (given by b.row and b.col , respectively).
{ b.setColor(current_color);
b.set(b.row, b.col, current_player); repaint(); }
The setColor and set method calls establish the color and then draw a value in the cell at b.row and b.col, given by the char variable current_player . Thus, the cell in row 4, column 1 is set to the value X in the above picture.
Now try making a series of additional selections and identify the places in the code of the BoardGame program that cause these selections to occur. As an exercise, try to achieve the following board display after a series of selections and moves.
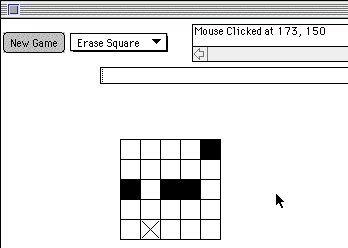
Answer the following questions before moving to Part 2.
The game should have a clear set of rules for defining when the game is over. Typically, a GameOver method can be written that interprets these rules and delivers a boolean value, true or false , depending on whether no further moves by either player can be made. At that point, your program should also report the identity of the winner (Player 1 or Player 2) or a tie game in the TextArea part of the frame.
The game should have a clear definition of what it means for a player to make a legal move and complete his/her turn. It should not allow illegal moves to be made. When one player completes a turn, the interaction should provide a prompt that tells whose turn is next. The variables that define the state of the game should include one whose value changes, say between 0 and 1, every time one player's turn ends and the other's is about to begin.
The interaction should report to the players, through the TextArea display, exactly what's going on as each move is made and each turn is completed. For instance, when Player 1 completes a turn, it should display a message like "Player 2's turn." When the game is over it should display a message like "Game over, Player 1 wins."

(A skeleton tic-tac-toe program is given in the files TicTacToe.java and TicTacToe.html inside the myApplet folder) Each player (Player X or Player O) takes a turn by clicking the mouse to place an X or O on one of the unoccupied squares; player X plays first. The winner is the player who first places 3 X's or 3 O's in a row, either horizontally, vertically, or diagonally. A tie game occurs when the board is full and noone has 3 X's or O's in a row.
The program should conduct a dialogue with the two players using the TextArea for displaying appropriate messages. It should allow each player to click on any empty square and replace that square with an X or an O (depending on whose move it is).
To monitor this game, your program should be able to
The state of the program should include, among other things, a variable whoseTurn which tells whose turn it is -- Player X or Player O -- and that variable should be changed whenever the mouseClicked handler determines that a player has concluded their turn.
Optional extra credit: Think of a straegy by which your program may assume the role of Player X and play a competitive game of Tic Tac Toe. (Do this part only after you have completed the basic part described above.)
o o o o o o o
o o o o o
o o o
Each player takes her turn by removing one or more pebbles from any one of the three rows. The winner is the player who picks up the last pebble. A Java program can monitor this game by displaying a 7x7 Grid in which the first three rows contain O's in locations where the pebbles are initially placed, as shown below:
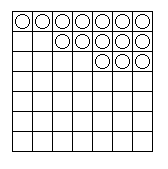
The program should conduct a dialogue with the two players using the TextArea for displaying appropriate messages. It should allow each player to click on the particular pebble(s) to be removed during that player's turn, but it should not allow a pebble to be picked up in two different rows during the same turn. To mark a "removed" pebble, the program should replace its O with an X on the same position of the board.
To monitor this game, your program should be able to
The state of the program should include, among other things, a variable whoseTurn which tells whose turn it is -- Player 1 or Player 2 -- and that variable should be changed whenever the musetClicked handler determines that a player has concluded her turn (clicked outside the board).
Optional extra credit: Think of a straegy by which your program may assume the role of Player 1 and play a competitive game of Nim. (Do this part only after you have completed the basic part described above.)

A square is filled in on the grid to indicate
a living individual, and is empty to indicate the absence of a living individual.
Each square on the grid has up to eight immediate "neighbors,"
one immediately on each side and one immediately on each diagonal. For
example, the eight neighbors of the cell at position (2, 3) -- that is, row
2 and column 3 -- are the cells at positions (1, 2), (1, 3), (1, 4), (2,
2), (2, 4), (3, 2), (3, 3), and (3, 4).
The play of the game is simply to track what happens to the grid from one generation to the next, over a series of generations. We start with an initial generation of individuals, such as the one shown in the lefthand grid below.
To predict which individuals will be living in the next generation, we apply the following rules to each cell in the lefthand grid.
Repeating this process over a series of generations gives some interesting patterns of population growth and decay. For instance, the pattern in the upper lefthand corner of the grid will repeat itself over a series of generations, while the one in the lower lefthand corner will completely disappear after the second generation. The pattern in the middle of the screen will change shape and position in an interesting way across a series of generations.
To visualize these population shifts, your interaction should provide two grids side-by-side on the board, and then ask the player to define the first generation by clicking on a series of squares in the lefthand grid. Completion of that activity may be signaled by the user's clicking outside the grid, or perhaps selecting a different alternative in a Choice menu on the screen. Next, the user should be able to ask the program to compute and display the second generation on the righthand grid, the third generation on the lefthand grid, the fourth on the right, and so on. The end of the simulation is reached by any one of the following events:
boolean runTheMaze from a given square
(x, y) {
set the current square to X and the
variable 'out' to false.
step forward
while (x, y) is not at the edge of
the grid {
turn right
while (facing a wall)
turn left
step forward
}
return out
}
Using the Grid class and the skeleton program boardgame.java , the following interaction can be used as a starting point for modeling and visualizing the maze-running process.
This particular grid was achieved by selecting the "Load grid from file" menu option, and then typing the name of the file "maze1" in the TextField window. This simplifies the process of initializing a maze by avoiding the need to mouse click in every square that should be turned ON. By convention, the maze itself is defined by the configuration of all grid squares that remain OFF.
A path through the maze can be represented by marking an "X" at each step of the path. A simple algorithm for following a path was discussed at the beginning of the semester. This algorithm is also discussed in your textbook.
There's another algorithm, which is recursive, that also does the job. Here is a summary of that algorithm, given a square in row x and column y on the grid and assuming that an adjacent square to the North, East, South, or West has not yet been visited.
boolean runTheMaze from a given square
(x, y) {
set the current square to X and the
variable 'out' to false.
if (x, y) is not at the edge of the
grid {
if the square immediately to the
West has not yet been visited,
out = run the maze from that
square
if not out and the square immediately
North has not yet been visited,
out = run the maze from that
square
if not out and the square immediately
East has not yet been visited,
out = run the maze from that
square
if not out and the square immediate
South has not yet been visited,
out = run the maze from that
square
}
else { out = true
we've run the maze!
}
return out
}
Modeling maze-running as an interaction
can allow the user to single-step the maze-running process, displaying the
new maze after each step is taken. The interaction may also identify steps
over squares already visited (this is called
"backtracking") by marking them with a different symbol, such as "O."
You can define any maze that you like, no matter how complicated or how large, by using the conventions shown in the file "maze1" and making your maze as a separate file. In a maze file, a wall is indicated by an asterisk '*' and an unoccupied square is indicated by a space ' '. Your maze file should have the same number of lines as it has characters in each line (that is, grids must be square). Just for variety, run your program with the alternative maze file "maze2".